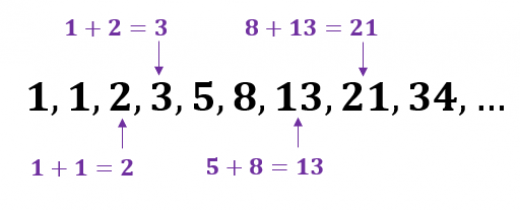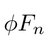【神秘的】『フィボナッチ数列と黄金比』はヒトに刻まれた美的感覚そして為替予測まで・・・すごい!
数学的解法」などの諸問題に対する解答も記している。この解答で使用された数列が後にフィボナッチ数列として知られるようになる数列である。この数列は、インドの数学者の間では6世紀頃から知られていたが、西洋に初めて紹介したのはフィボナッチの書いた算盤の書である。 『算盤の書』は次の15章からなる。 インド・アラビア数字の読み方と書き方 13キロバイト (1,549 語) - 2021年7月2日 (金) 14:04 |
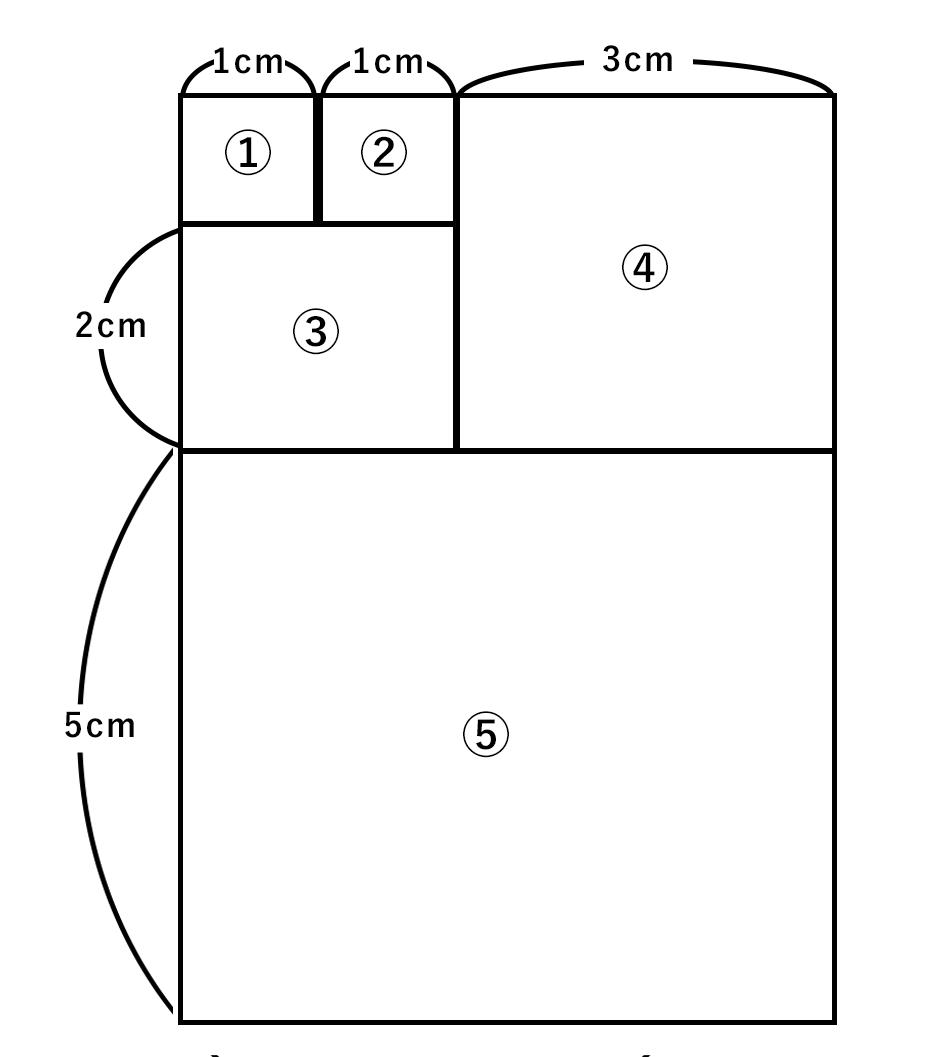
フィボナッチ数列とは、0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …のような数のことを言い、この数列に潜む規則性は、となりあう3つの数において、左2つの数の和が右の1つの数になるというものです。
自然界には黄金比やフィボナッチ数列で構成されたものがたくさんあり、有名なピラミッドの建築も黄金比、フィボナッチ数列で できているんですね。
他にも「ミロのヴィーナス」、「モナ・リザ」、「パルテノン神殿」、「サクラダ・ファミリア」、エジプトの「ピラミッド」など古代より西洋の美術作品や建築物などに取り入れられています。
この数字が自然界に多く潜んでいるという現実も、とても神秘的なことです。
<関連する記事>
 | 【フィボナッチ数列と黄金比】花びらにも!? 自然界に多く登場する魔法の数列と究極の比 …φ=(1+√5)/2=1.618... ---------- フィボナッチ数列の規則性とは フィボナッチ数列とは、以下のような数列のことをいいます。 0, 1… (出典:現代ビジネス) |
 | 終電の席を譲った女性、席を断った中年、席を奪ったのは【精神科医が解説】 …運動をすることを発見した。DNAも螺旋であり、最も美しいといわれるフィボナッチ数列も螺旋を表現している。螺旋こそが生成のための基本原理であり最高の効率… (出典:幻冬舎ゴールドオンライン) |
 | 次世代シミケア「フィボナッチ」と五感エイジングケア「エレミス」が推せる! …的な繁栄をもたらす奇跡のパターン「フィボナッチ数列」が似ていることから名づけられたそう。 容器にはフィボナッチ数列が表す黄金比をちりばめてあり、構造美… (出典:@BAILA) |
 | 月利200万円稼ぐギターの先生、FXで500万円溶かして気づいたこととは …のトレーダーの間で話題の『ハーモニックパターン』を利用しています。フィボナッチ数列から導き出される黄金比は相場の節目を探すために広く利用されてきました… (出典:週刊SPA!) |
 | 相場が、なぜ、5つの波と3つの波からできていると考えられているのか。 …が、以前にお伝えした「フィボナッチ数列」にその答えが隠されています。 ○フィボナッチ数列 ※筆者作成 フィボナッチ数列は、イタリア人数学者レ… (出典:ファイナンシャルフィールド) |
<関連する画像>
<関連する動画>
<ツイッターの反応>
数学bot
@bot34701280フィボナッチ数列の性質22つの自然数pとqの最大公約数がrならばF〔p〕とF〔q〕の最大公約数はF〔r〕である。mがnで割りきれるのならば、F〔m〕はF〔n〕で割りきれる。n、n+1は互いに素であることより、F〔n〕とF〔n+1〕は互いに素である
アオミドロ改
@aomidoro__5813フィボナッチ数列…最初の二項は0,1と定義され、以後どの項もその前の2つの項の和となっている。(0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…)隣り合うフィボナッチ数の比は黄金比 φ に収束する。
1時間に1回叫ぶ淵野アタリbot
@ebifrie_ガパオライスクソ辛いス、でもこれは8万のイス!あ、加えたエタノール、クワとエタノール!クロマニヨン人をすり潰してクロマトグラフィーするぞ!*電車略して沈殿!お!これ5の次8だからフィボナッチ!でも次9だから違うや、ボッタクリ数列 あ、5の次6って知ってましか?
ナルトのなる
@narutononaru自然界には黄金比やフィボナッチ数列有名なピラミッドの建築も黄金比、フィボナッチ数列でできているんですね。0から始まり0, 1, 1, 2, 3, 5, 8, 13, 21このフィボナッチはFXでも使います。#FX #フィボナッチ #フィボナッチ数列
👖👟ワームホール🏎🐟
@hiro_wormhole@SuzukiRC1 おぉ!フィボナッチ数列!ひまわり然り、自然界での数列の美しさは素晴らしいですよね
嵐のFX 勉強部屋
@FXarashi_world@kapio_fx これは世の中全てのものに共通するフィボナッチ数列の黄金比です😊 https://t.co/4c7RAfDB4r
フィボナッチ数列 bot
@Aureus_Nフィボナッチ数の積の数列の漸化式-3. https://t.co/GfAnlnM3Gs
ちゃたん
@XDDYybWbLb2fkEIフィボナッチ数列ときくと貝殻に乗ったヴィーナスが横切っていく。うららか〜🌸どうしてかと思ったらフィボナッチ→ボッティチェリの連想なんだな。こんな母の子でもフィボナッチ数列しなくちゃいけないの?🥺😢
あんみん
@shinbiganA#FlowerOfLife #神聖幾何学#トーラス万物の創成を解き明*鍵とは?生命の神秘も元素の仕組みもギリシャの神聖幾何学にヒントが隠されていた黄金比、フィボナッチ数列、メタトロンキューブフラワーオブライフ… https://t.co/R0RIEv07Xf
フィボナッチ数列 bot
@Aureus_Nフィボナッチ数の三乗を並べた数列の漸化式. https://t.co/2LrlfHNMP8
白玉さおりん
@shira_saori【フィボナッチ数列】1,1,2,3,5,8,13,21,…というふうに連続した2つの数字を足すとその次の数字になるような数列を「フィボナッチ数列」と呼ぶの☆ 一般項は「a_n=[{(1+√5)/2}^n - {(1-√5)/2}^n] /√5」…分かりづらい?
ピロ
@panda23_fxエリオット波動の考えはフィボナッチリトレースメントフィボナッチ時間数列はあてつけや、後からのこじ付け論に過ぎない偶然の産物とあります。確かに証券会社で違うしなので、ウォルフターゲットの位置も❓但し現在はフィボナッチ数列とエ… https://t.co/6OuXbzvnyO
きらきら研修医
@Dr_kirakiramie【フィボナッチ数列と黄金比】花びらにも⁉ 自然界に多く登場する魔法の数列と究極の比 https://t.co/REkFQbmSjl #ブルーバックス
シン・朝倉
@tompockleテストケースとしてフィボナッチ数列を求める処理が用意されていて、ただでさえ苦手な再帰呼出しのコールスタックを手で書き出すという作業をすることになったのが結果的に結構勉強になった気がする
くむ
@kumkum__fdgk0フィボナッチ数列って可愛いいい名前してる
かわせなち👾💤
@XxkawasexX@Katsuobushi1127 単元やないけどフィボナッチ数列
ホニャラカ
@honyarakasan【フィボナッチ数列と黄金比】花びらにも⁉ 自然界に多く登場する魔法の数列と究極の比 https://t.co/gJMn0B7r5B #ブルーバックス
こじ
@subarasiitabi@mkr_prfm 素数なうえにフィボナッチ数列で強すぎる負けました
物理の雑学@相互フォロー
@marblephysics【フィボナッチ数】n番目のフィボナッチ数をF_nとするとF_0=0F_1=1F_(n+2)=F_(n+1)+F_nつまり、0、1、1、2、3、5、…となる数列のことである。フィボナッチ数は自然界にも多く現れており、例えば花びらの数はフィボナッチ数であることが多い。
数学bot
@bot34701280フィボナッチ数列の性質3F〔n〕をn番目のフィボナッチ数とする。lim〔n→∞〕F〔n〕/F〔n-1〕=φ。φは黄金数F〔m〕が偶数となるのはmが3の倍数となるときと一致F〔m〕が5の倍数となるのは mが5の倍数となる… https://t.co/DmOGoerAkM